Die folgenden Abbildungen sind mit dem Computer-Algebra-System
"Derive" erzeugt. In der Lernumgebung
"Modellieren mit Mathe" gibt es Anleitungen
zu Derive:
In dieser Lernumgebung gibt es einführende
Crash-Kurse
zum Werkzeug Excel, um Funktionen direkt
zeichnen zu können.
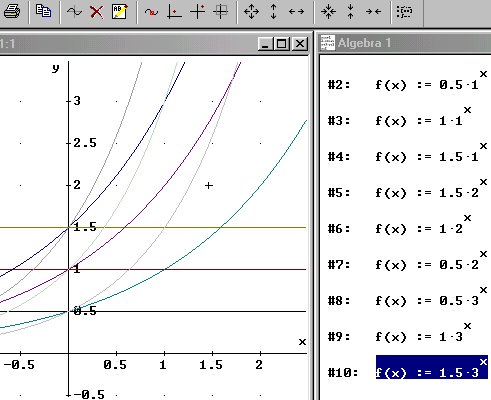
Exponentialfunktion: f(x) = c ·
a x
In den nachfolgenden Abbildungen wurden für
die Formvariable a die natürlichen Zahlen
1; 2 und 3 eingesetzt und konstant gehalten. Für
die Formvariable c wurden dann jeweils die Zahlen
0,5; 1 und 1,5 eingesetzt. Was fällt an Besonderheiten
oder Regelmäßigkeiten auf?
|
|
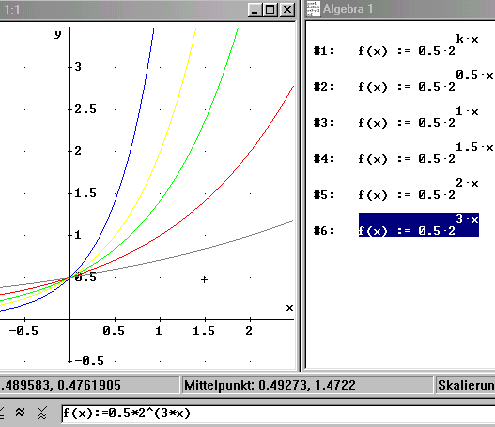
Exponentialfunktion: f(x)
= c · a k·x
Für die Formvariable
c wurde 0,5 und für die Formvariable a wurde
2 gewählt und konstant gehalten. Sodann wurden
für die Formvariable k nacheinander die Zahlen
0,5; 1, 1,5; 2 und 3 gewählt. Was bewirkt
die Veränderung des Parameters k ?
|