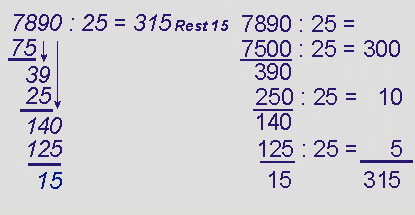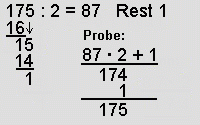Ideen für mögliche, selbstorganisierte
Übungen:
|
Dividend:Divisor=Quotient
|
|
|
- Erläutert in eurer Kleingruppe, wie ihr
bei den vorstehenden Divisionen rechnen dürft
und könnt.
- Schätzt die Divisionen (Quotienten) nach
oben und unten ab.
- Argumentiert an diesen Beispielen aber auch,
warum ihr so rechnen dürft.
Gebt euch in eurer Kleingruppe nun gegenseitig
schriftliche Divisionsaufgaben vor, wobei mehrstellige
Zahlen durch ein- und zweistellige Zahlen dividiert
werden sollen.
- Führt das schriftliche Rechenverfahren
jeweils aus und schätzt auch die Divisionen
nach oben und unten ab.
- Rechnet jeweils alle Divisionen auch ausführlich
mit Proben, so wie oben vorgeführt.
- Überprüft euch gegenseitig, indem
ihr euch den Rechenverlauf vorsagt. Nutzt bei
der Überprüfung eures Ergebnisses
einen Taschenrechner.
|