|
|
Parallel zueinander - eine Erklärung
|

|
|

|
|

|
|

|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Voraussetzung
|
|
|
| |
|
|
|
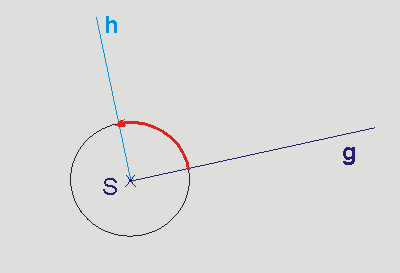
Zur Erinnerung:
Bildet eine Halbgerade g mit einer anderen Halbgeraden
h einen Winkel von 90° und schneiden sie sich
im Punkt S, so sagt man: g steht
senkrecht auf h im Punkt S.
|
|
|
| |
|
|
|
Erklärung von
"parallel zueinander"
durch eine Konstruktionsvorschrift:
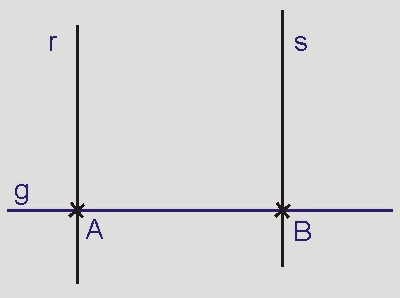
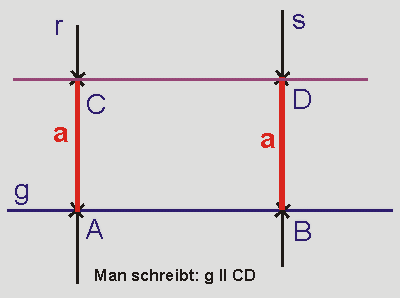
Gegeben seien:
Die Gerade g und auf ihr die Punkte A und B;
die Gerade r, die senkrecht auf g im Punkt A steht;
die Gerade s, die senkrecht auf
g im Punkt B steht.
|
|
 |
|
| |
|
|
|
|
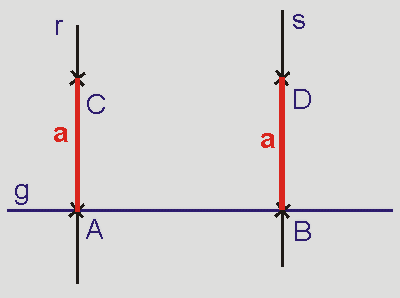
Auf den Geraden r und
s werden nun von A und B aus dieselben Strecken
a (rot) abgetragen. So entstehen
die Punkte C und D auf den
Geraden r und s.
|
|
 |
|
| |
|
|
|
Die Gerade CD (violett)
ist dann eine Parallele zu g im Abstand a.
Folgerung: Sind zwei Geraden
parallel zueinander,
so haben sie überall den gleichen Abstand.
Somit kann man auch erklären:
Zwei Geraden, die überall denselben Abstand
haben, sind parallel zueinander.
|
|
 |
|
| |
|
|
|
|
|
|
| |
|
|
|
Ideen für mögliche,
selbstorganisierte
Übungen:
|
|
- Argumentiert: Wenn AB
 CD so ist auch CD
CD so ist auch CD  AB
AB
- Argumentiert: Zwei Geraden, die auf einer
anderen senkrecht stehen, sind parallel.
- Argumentiert: Die kürzestes Entfernung
zwischen zwei parallelen Geraden ist der Abstand
zwischen den Parallelen.
- Euklid (330 - 275 v.Chr.)
erklärte grundsätzlich:
Zwei Geraden in einer Ebene, die sich
nicht schneiden, sind parallel.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
© Pädagogisches
Institut für die deutsche Sprachgruppe Bozen 2000 -
. Letzte Änderung:
08.05.2013
|
 |
|
|
|