|
|
Ihr habt bei eurer Arbeit an realen Problemen u.a. die folgenden und weitere rationalen Abhängigkeiten kennengelernt. |
|
|
|
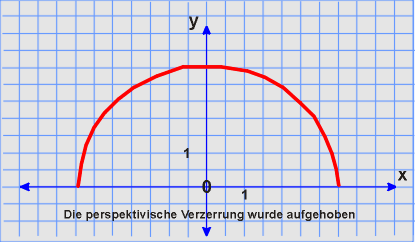
Der Bogen
der Brücke Espalion
|
|
 |
| |
|
|
| |
|
x |
- 3,5 |
- 2 |
- 1 |
0 |
1 |
2 |
3,5 |
y |
0 |
2,9 |
3,4 |
3,5 |
3,4 |
2,9 |
0 |
|
| |
|
|
Die Funktionsgleichung zur
Brücke in Espalion |
|
Abstrahieren wir von den Bedeutung tragenden Längen und schreiben wir für die unabhängige Variable immer die Leerstelle (Variable) x und für die abhängige Variable immer die Leerstelle (Variable) y, so lautet die Funktionsgleichung:
|
| |
|
|
| |
|
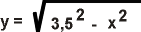
Die Umkehroperation des Quadrierens ist das Radizieren (das "Wurzelziehen"). So sind die Umkehrfunktionen der quadratischen Funktion die Wurzelfunktionen. |
| |
|
|
|
|
|
| |
|
|
Die Funktionsgleichung zur
Abhängigkeit der
Leistung P von der Zeit t |
|
Abstrahieren wir von den Bedeutung tragenden Größen (der Zeit t und der Leistung P) und schreiben wir für die unabhängige Variable immer die Leerstelle (Variable) x und für die abhängige Variable immer die Leerstelle (Variable) y, so lautet die Funktionsgleichung:
y = 80J : x |
| |
|
|
| |
|
Eine nochmalige Abstraktion von den konstanten Größen führt dann zu folgenden Gleichungen mit Formvariablen oder zu den folgenden Gleichungen mit Parametern. |
| |
|
|
| |
|
y = a : x + b oder f(x) = a : x + b
|
| |
|
|
| |
|
Die Grafen der Funktionen y = a · (1/x) + b heißen Hyperbeln. |
|
|
|
|
|
|
| |
|
|
| |
|
Abstrahieren wir auch hier von den Bedeutung tragenden Größen und schreiben wir für die unabhängige Variable immer die Leerstelle (Variable) x und für die abhängige Variable immer die Leerstelle (Variable) y, so erhalten wir wiederum nach einigen weiteren Verallgemeinerungen u.a. Funktionsgleichungen der folgenden Art: |
| |
|
|
| |
|
y = (x+a)(x+b)(x+c) oder y = ax³ + bx² +cx + d |
| |
|
|
| |
|
Funktionen dieser Art heißen Funktionen dritten Grades oder Polynomfunktionen dritten Grades. Entsprechend lassen sich die Funktionen der Formen vierten ... bis n-ten Grades formulieren. |
| |
|
|
Beispiel: Potenzfunktionen |
|
Eine Fortsetzung der vorstehenden Abstraktionen führt jeweils zu unterschiedlichen Gruppen von Funktionsgleichungen so z.B. auch zu Funktionsgleichungen bei der die unabhängige Variable x die Basis einer Potenz ist (und der Parameter n Element der Menge der natürlichen Zahlen, die Parameter k und u Elemente der Menge der reellen Zahlen und der Parameter r Element der Menge der rationalen Zahlen ist).
f(x) = k · x^n
f(x) = x^n + u
f(x) = k · x^r, r > 0
f(x) = k · x^r, r < 0 |
| |
|
|
| |
|
|
