| |
|
|
Wortmodell, Modellannahme |
|
Bereits Infizierte werden nach einer gewissen Zeit (Inkubationszeit) krank. Alle Kranken und Infizierten stecken immer wieder noch nicht Infizierte an. |
| |
|
|
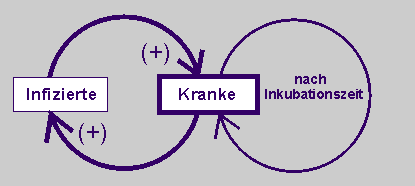
Wirkungsdiagramm |
|
 |
| |
|
|
Qualitative Beschreibung |
|
Die Zahl der Kranken wirkt positiv auf die Zahl der Infizierten: Je mehr Kranke es gibt, desto mehr Menschen können infiziert werden, desto mehr Infizierte wird es geben und desto mehr werden krank. |
|
|
|
Abstraktion oder Bestimmung der Zustandsgröße, Flussgröße und Parameter |
|
Die Zustandsgröße Kranke (K) ist leicht zu erkennen. Flussgröße ist die Zahl der Infizierten (I). Auf sie wirkt eine Infektionsrate (r) und die Zahl der bereits Kranken.
Die Infizierten werden erst nach einer Inkubationszeit krank. Diese bleibt hier unbeachtet. Siehe hierzu aber gegebenenfalls "Ideale Modelle zur Ansteckungs- und Abklingphase eines Infekts" in der Lernumgebung "Mathe Überall". |
| |
|
|
Flussdiagramm und Quantifizierung |
|
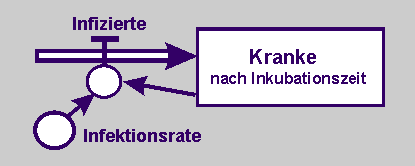 |
| |
|
|
Zustands- und Modellgleichung |
|
Kranke_neu < -- Kranke_alt + Δt · Infizierte;
Anfangsgröße K = 3
Δt = 1, (Zeittakt 1Tag)
Infizierte = Kranke · Infektionsrate
Infektionsrate r = 0,1
|
| |
|
|
Programmierung mit Excel |
|
Siehe hierzu:
ExcelDateien/Mappe1628a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1628a.xls (herunterladbar und interaktiv)
Anmerkung: Zur Programmierung siehe: Crash-Kurse: Einführung in die Nutzung von Excel |
| | |
|
Eine Simulation
(sie passt zu den obigen Modellgleichungen)
Wird die Infektionsrate erhöht, so ergibt sich bei gleich bleibender Anfangsgröße schnell ein völlig anderes Bild. Erst recht steigt die Zahl der Kranken rasend schnell, wenn auch noch die Anfangsgröße erhöht wird.
|
|
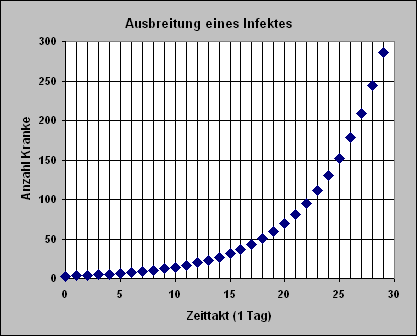 |
| |
|
|
Verhaltensbeschreibung, Zweck und Grenzen des Modells |
|
siehe unten als Aufgabe.
|
|
|
Wie ändert sich aber die Anzahl von Gesunden, Kranken und schließlich von Immunen bei einer Epidemie?
|
| |
|

|
Wortmodell und qualitative Beschreibung |
|
Gesunde werden infiziert und dann krank. Kranke erholen sich, werden geheilt und sind dann für eine Zeit immun gegenüber der infektiösen Krankheit. Diese Wirkungen sind positiv.
Aber je mehr Kranke es gibt, desto weniger Gesunde wird es geben. Die Anzahl der Kranken wirkt negativ auf die Anzahl der Gesunden. Entsprechend wirkt die Anzahl der Immunen auf die Anzahl der Kranken.
Das folgende Wirkungsdiagramm beschreibt die Zusammenhänge qualitativ. Es wird also gefragt, Was wirkt auf Was und wie. Argumentiert wird mit dem Plus- oder Minuszeichen oder mit „je desto“. |
| |
|
|
| |
|
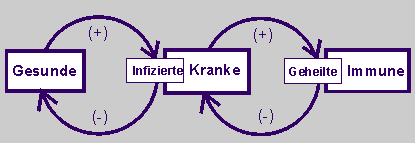 |
| |
|
|
Abstraktion oder Bestimmung der Zustandsgrößen, Flussgrößen und Parameter |
|
Bei einer Quantifizierung des Wirkungsdiagramms in das folgende Flussdiagramm sind die Gesunden (Ges), Kranken (Kra) und Immunen (Imm) die Zustandsgrößen. Sie sind quasi hintereinander geschaltet. Die Zahlen folgen auseinander.
Die Zahl der Infizierten (In) und die der immer wieder Geheilten (Ge) sind die Flussgrößen. Auf die Flussgröße der Infizierten wirken die Infektionsrate (ir) und der Zahl der Gesunden. Entsprechend wirken auf die Zahl der Geheilten die Heilungsrate (hr) und der Zahl der Kranken. |
| |
|
|
Flussdiagramm und Quantifizierung |
|
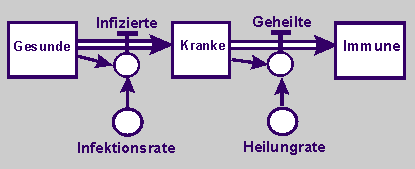 |
|
|
|
Zustands- und Modellgleichung |
|
Ges_neu <-- Ges_alt + Δt · (-In);
Anfangsgröße: Ges = 5000; Δt = 1; (Zeittakt: 1 Tag oder 1 Woche ...)
Kra_neu <-- Kra_alt + Δt · (In - Ge);
Anfangsgröße: Kra = 0 ; Δt = 1; (Zeittakt: 1 Tag oder 1 Woche...)
Imm_neu <-- Imm_alt + Δt · (Ge);
Anfangsgröße: Imm = 0; Δt = 1; (Zeittakt: 1 Tag oder 1 Woche...)
In = Ges · ir; Infektionsrate: ir = 0,1;
Ge = Kra · hr; Heilungsrate: hr = 0,035
Woher die Werte für die Raten kommen, das siehe unter Sach-Informationen zu Grippen, SARS und andere viröse Krankheiten). Im vorstehenden Modell werden die Infektions- und Heilungsrate als nahezu gleich angenommen. Die Heilungsrate „hinkt“ im obigen Modell aber etwas hinter der Infektionsrate her.
Allgemein gilt, dass die Infektions- und Heilungsrate vom Typ der Epidemie abhängen aber auch voneinander abhängen können. Es ist z.B. ein Unterschied, ob sich eine normale Grippe oder AIDS oder SARS ausbreitet. |
| |
|
|
Programmierung mit Excel |
|
Siehe hierzu:
ExcelDateien/Mappe1628b.htm (nur zur Ansicht) oder ExcelDateien/Mappe1628b.xls (herunterladbar und interaktiv)
Die Zahl der Infizierten und Geheilten ist jeweils auf null Stellen hinter dem Komma gerundet. Mathematisch ist das ein Fehler, interpretativ gibt es aber nur ganze Menschen! |
|
|
|
Eine Simulation
(sie passt zu der obigen Gleichungen
In der Tabelle lassen sich die Anfangsgrößen und Raten sowie Delta t ändern. Geschieht dies, so ergibt sich jeweils ein anderes (ggf. auch nicht mehr interpretierbares) Simulationsergebnis.
Eine Anleitung zur
Entwicklung dieses Modells mit
INSIGHT MAKER
findet Ihr hier. |
|
 |
| |
|
|
Verhaltensbeschreibung, Zweck und Grenzen des Modells |
|
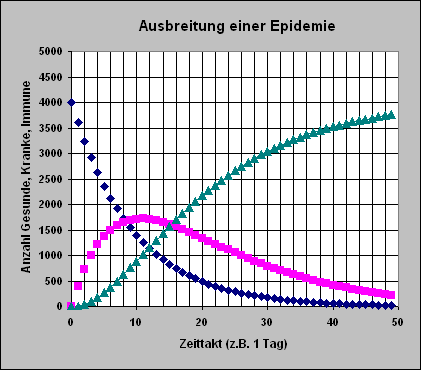
In diesem dynamischen Modell der Ausbreitung einer Epidemie nimmt die Zahl der Gesunden in der ersten Zeit schnell ab und nähert sich dann langsam nahezu der Null. Alle werden krank. Die Zahl der Kranken steigt schnell auf einen Höchstwert, nicht ganz halb so groß, wie der Anfangswert der Gesunden. Dann sinkt die Zahl der Kranken - langsamer werdend - auch gegen Null ab. Die Zahl der Immunen steigt zunächst schnell an und strebt dann langsamer werdend einem Höchstwert zu, der dem Anfangswert der Gesunden entspricht. Schließlich sind alle Kranken immun geworden, also wieder gesund.
Wird Delta t verkleinert, so zieht sich der beschriebene Prozess über eine längere Zeit hin. Der gesamte Zeitablauf wird verzögert.
Die Modellierung endet also - nach einer quantitativen Zwischenphase - mit einer Verhaltensbeschreibung, die wieder qualitativ ist. Das ist in diesem Fall aber der Zweck des Modells. Es vermittelt die grundlegende (qualitative) Einsicht : So läuft generell eine Epidemie ab! Sollen quantitative Prognosen erstellt werden, müssen die Infektions- und Heilungsrate zum Typ der Epidemie passen. |
|
|
|
Eine mögliche zweite Modellerweiterung |
|
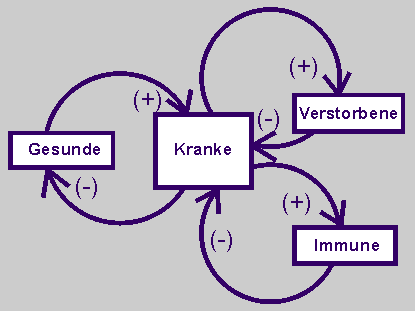
Aber in diesem Modell erkranken alle Gesunden und werden schließlich immun. Das muss aber so nicht sein. Es gibt z.B. auch Ausbreitungen von Viren, die zum Tod führen. Hier liegt also eine Grenze des Modells. |
| |
|
|
Wirkungsdiagramm zu einer möglichen Modellerweiterung |
|
 |
| |
|
|