blikk

Herausforderung: technisch-medialer Wandel
forum galerie sitemap
punkt infothek
blikk schule

Ein einfaches Neuronales Netz:
auf der Grundlage des Perceptions-Modells

an den anfang zurueck weiter ans ende eine ebene nach oben
     

Ein einfaches Abbildungsbeispiel

Die drei Muster A, B und C sollen erkannt werden und eine je spezifische Reaktion zur Folge haben.
Wenn das Muster A erkannt wird, so soll Outputneuron 1 "aktiv" sein (den Befehl zum Wegspringen geben),
wenn Muster B erkannt wird, so soll Outputneuron 2 "aktiv" sein (den Befehl zum Angriff geben) und entsprechend soll Outputneuron 3 "aktiv" sein (den Befehl zum Nichtstun geben), wenn das Muster C erkannt wird.

  

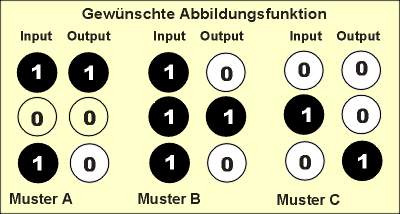
Mathematisch handelt es sich um eine Abbildungsfunktion, die sich auch
vektoriell wie folgt schreiben lässt:
(101) --> (100), (111) --> (010), (010) --> (001)
...    
Lösung des Abbildungsproblems mit Hilfe eines Programms in einer seriellen Schrittfolge Ein seriell arbeitender Computer, etwa ein PC, würde das Problem mit folgendem Programm lösen:
Gehe zum mittleren Input-Neuron und stelle fest, ob es feuert oder nicht; feuert es nicht, so handelt es sich um Muster A, feuert es, so gehe zum oberen Input-Neuron; feuert dies nicht, so handelt es sich um Muster C; feuert es , liegt Muster B vor.
Dieses ist noch ein einfaches Programm mit Rechen- und Zuordnungsregeln. Mit jedem zusätzlichen Abbildungspunkt wird das Programm aber exponentiell komplizierter.
     

Lösung des Abbildungsproblems mit Hilfe eines einfachen Neuronalen Netzes

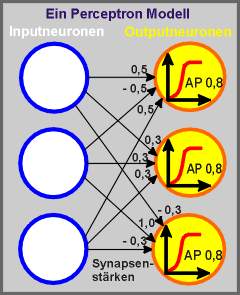
In einem Perception Modell ist jedes Neuron der Inputschicht mit jedem Neuron der Outputschicht verbunden. Jeder einzelne Input wird gewichtet und gelangt so in die Outputschicht. Annahme: Alle drei Outputneuronen haben ein Aktivierungspotential von 0,8.

 
..    

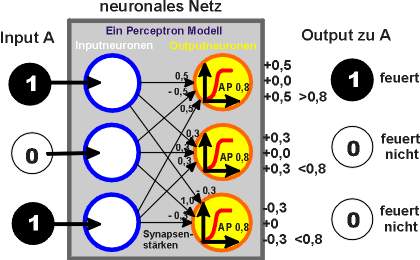
Beispielrechnung für die Abbildung von Muster A

Wird Muster A wahr-genommen, entspricht die Aktivität der Inputschicht diesem Muster. Über die Verbindungen erhalten alle Neuronen der Outputschicht - mit unterschiedlichen Synapsenstärken gewichtet - diesen Input. Das obere Neuron der Outputschicht erhält über seine Synapsen den Gesamt-Input 1. Er ist größer als das AP von 0,8, also feuert das oberste Outputneuron. Der entsprechend berechnete gewichtete Input des mittleren Neurons beträgt 0,6 der des unteren Neurons -0,6. Also sind diese beiden Neuronen nicht aktiv.

 




     

Ein neuronales Netz verarbeitet alle eingehenden Inputs parallel (gleichzeitig).

 

Neuronale Netze können trainiert werden, sie sind lernfähig und können insbesondere die Synapsenstärken selbständig lernen.

  

Die Verarbeitung aller Inputs erfolgt parallel: gleichzeitig in allen drei Neuronen der Outputschicht. Diese Parallelverarbeitung hat wesentliche Vorteile gegenüber der seriellen Arbeit. So erfolgt das Erkennen des Musters in einem einzigen Schritt. Besteht also das Muster aus mehr als drei Bildpunkten, bleibt die Schnelligkeit erhalten. Das Erkennen komplexerer Muster erfordert also lediglich mehr Neuronen. Das Wissen über die richtige Zuordnung oder Abbildung steckt im Netz, also erstens in der Art der Vernetzung der Neuronen, zweitens insbesondere in der Stärke der Synapsen und drittens im Aktionpotential.
Wenn wir davon ausgehen, dass unser Gehirn eher wie ein neuronales Netz funktioniert - und nicht seriell wie ein herkömmlicher Computer arbeitet - dann erscheinen geistige Prozesse in einem neuen Licht. Ebenso wird deutlicher, was damit gemeint ist, wenn gesagt wird: das wurde in der biologischen Evolution gelernt.
an den seitenanfang