| |
|
|
Wirkungsdiagramme zum Bevölkerungswachstum
Quelle: Die Grenzen des Wachstums, Seite 26ff |
|
 |
| |
|
|
| |
|
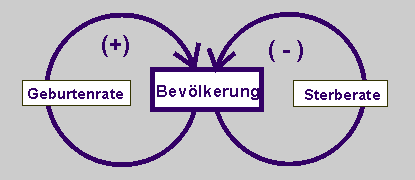
Bei Vernachlässigung der Größen Fruchtbarkeit und Sterbeziffer kann das Wirkungsdiagramm auch wie folgt aussehen: Es besteht aus zwei Rückkopplungskreisen. Der eine ist positiv. Je mehr Menschen leben, umso mehr Kinder werden bei gegebener Geburtenrate geboren. Der andere Rückkopplungskreis ist negativ. Je mehr Menschen leben, umso mehr werden sterben, bei gegebener Sterberate. |
|
|
|
Analyse der wirkenden
Zustands- und Flussgrößen |
|
 |
| |
|
|
| |
|
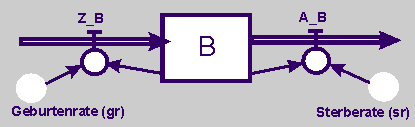
Es gibt also eine Zustandsgröße, die Bevölkerung (B). Auf diese wirken zwei Flussgrößen. Die Zunahme_Bevölkerung (Z_B) ist eine positive und die Abnahme_Bevölkerung (A_B) eine negative Rückkopplung. Die beiden Raten wirken ihrerseits auf die Flussgrößen. Mittels dieser Quantifizierung entsteht das folgende Flussdiagramm. |
| |
|
|
|
|
 |
| |
|
|
"Abstraktion" der Zustandsgleichung und
der beiden weiteren Modellgleichungen |
|
B_neu <-- B_alt + Δt · (Z_B - A_B)
Anfangsgröße Bevölkerung B = 82218 (Deutschland im Jahr 2007);
Δt = 0,002; (1 Zeittakt = 1 Jahr)
Z_B = B · gr Λ A_B = b · sr
In Deutschland 2007:
Lebendgeborene = 8,3 je 1000 Einwohner
Gestorbene = 10,1 je 1000 Einwohner
gr = 8,3 / 1000 = 0,0083 Λ sr = 10,1 / 1000 = 0,0101
|
| |
|
|
Programmierung der Gleichungen in einer Excel-Tabelle |
|
Siehe hierzu:
ExcelDateien/Mappe7660a.htm (nur zur Ansicht) oder ExcelDateien/Mappe7660a.xls (herunterladbar und interaktiv) |
| |
|
|
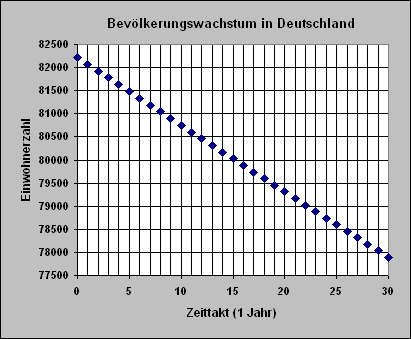
| Simulationsergebnisse
In dem Modell wird angenommen, dass es keinen Zuwachs durch Migration gibt.
Wachstum der Bevölkerung
in Deutschland ab dem
Jahr 2007
in den nächsten
30 Jahren,
bei einer gleich bleibenden
Geburten- und Sterberaten
wie im Jahr 2007.
| |
 |
| |
|
|
| |
|
Siehe hierzu:
ExcelDateien/Mappe7660b.htm (nur zur Ansicht) oder ExcelDateien/Mappe7660b.xls (herunterladbar und interaktiv) |
| |
|
|
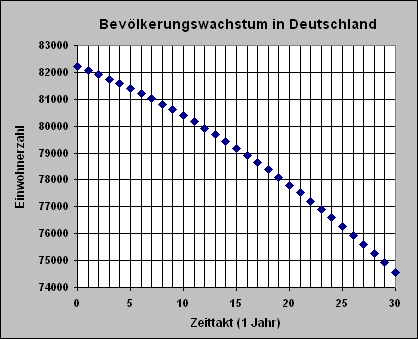
Wachstum der Bevölkerung in Deutschland ab dem Jahr 2007
in den nächsten 30 Jahren,
bei einer zeitabhängigen Geburtenrate, die sich zeitabhängig linear verkleinert.
|
|
 |
| |
|
|
| |
|
|
| |
|
|
Verweis auf ein Beispiel von Schülerinnen und Schülern
aus der Projektzeit 2002 |
|
Wir (isolde, martina, hannes, christoph und florian, 5 Schüler/innen der Klasse 5A des naturwissenschaftlichen Lyzeums "J. Ph. Fallmerayer" in Brixen) haben uns mit der Bevölkerungsentwicklung in Südtirol unter zwei verschiedenen Gesichtspunkten beschäftigt::
- Analyse der erfolgten Bevölkerungsentwicklung zwischen 1940 und 2000 am Beispiel zweier Gemeinden, nämlich Brenner (Abwanderungsgemeinde) und Eppan an der Weinstraße (Zuwanderungsgemeinde) (Quelle: Statistisches Jahrbuch 2001)
- Erstellung eines Modells mit Dynasys, um eine mögliche zukünftige Bevölkerungsentwicklung in Südtirol darzustellen.
Der zweite Teil wird unter Schülerarbeiten vollständig dargestellt. Die Jugendlichen haben das Werkzeug Dynasys benutzt. |
| |
|
|
| |
|
|
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
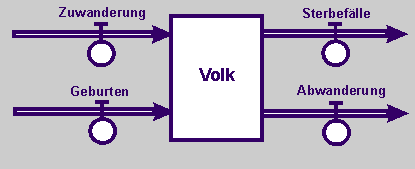
- Simuliert das Wachstumsmodell für Deutschland unter der Annahme unterschiedlicher Szenarien.
- Simuliert das folgende Wachstumsmodell für Deutschland und nehmt an, dass die Bevölkerung auch durch Migration wachsen bzw. fallen kann.
|
| |
|
 |
| |
|
|
| |
|
- Simuliert das Wachstumsmodell für ein Industrie-, Schwellen- oder Entwicklungsland und nehmt an, dass die Bevölkerung auch durch Migration wachsen bzw. fallen kann.
- Stellt die Entwicklung der Geburten- und Sterberaten ebenfalls durch ein Punkt-Diagramm dar.
- Approximiert die Entwicklung der Geburten- und Sterberaten durch lineare Trendlinien (Wachstumsfunktionen).
- Erweitert das Modell, indem ihr für die beiden Raten die Wachstumsfunktionen eingebt.
- Erweitert das Modell, indem ihr die beiden Raten zu Zustandsgrößen erklärt, stellt das erweiterte Modell in einem Flussdiagramm dar und programmiert das Wachstumsmodell in einer Exceltabelle.
- Simuliert das neu programmierte Wachstums-Modell.
- Diskutiert miteinander die Simulationsergebnisse und schreibt eure Einsichten auf.
- Diskutiert die Modellierung von isolde, martina, hannes, christoph und florian.
|