Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen (8) 9 bis 12 |
| |
|
|
Hinweise:
Die Bearbeitung der folgenden Aufgaben zur "Konstruktion und Simulation von dynamischen Wachstumsmodellen" kann Teil einer Gesamtlösung von arbeitsteilig arbeitenden Gruppen sein.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgenden Lösungen zur Konstruktion und Simulation
können in drei arbeitsteiligen Kleingruppen der Klasse erarbeitet werden.
Sie können Teil einer Gesamtlösung sein, bei der weitere Kleingruppen parallel arbeiten an der Konstruktion und Simulation dynamischer Wechselwirkungen zwischen Spinnmilben und Raubmilben.
Nach der Präsentation der Gruppenlösungen in der Klasse wird gemeinsam über den Zweck dynamischer Modellierungen diskutiert.
Für die Erarbeitung der nachfolgenden Teil-Lösungen und deren Formulierung sind etwa 4 - 5 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist sehr sinnvoll. Für eine Diskussion in der Klasse sind dann noch einmal 1 - 2 Schulstunden notwendig.
|
|
|
|
|
|
|
|
|
Gleichförmige und unbegrenzte Wachstumsmodelle
am Beispiel von Spinnmilben |
| |
|
|
| Beschreibt ein gleichförmiges und unbegrenztes Wachstums der Spinnmilben in Wirkungsdiagrammen. |
|
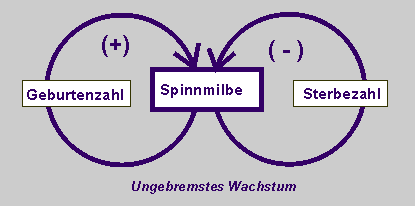
Wir nehmen an, dass die Spinnmilben in einer Gewächshausplantage genügend Nahrung in Form von Gurkenblättern haben. Dann nimmt die Spinnmilbenpopulation ständig zu, sehr zum Ärger des Plantagenbesitzers.
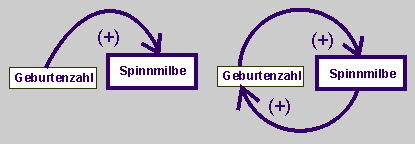
Der erste Schritt im Prozess der dynamischen Modellierung ist dann eine qualitative Beschreibung des Wachstums der Spinnmilben in einem Wirkungsdiagramm. Dabei fragen wir: Was wirkt auf Was ein und wie?
So zeigt das erste Wirkungsdiagramm, wie die Geburtenzahl der Spinnmilben positiv auf die Anzahl der Spinnmilben wirkt. Oder anders formuliert: Über die Geburtenzahl wächst die Spinnmilbenpopulation gleichförmig an.
Das zweite Wirkungsdiagramm zeigt, dass die zunehmende Anzahl der Spinnmilben auch positiv auf die Geburtenzahl zurückwirkt. Denn je mehr Spinnmilben leben, desto mehr Geburten wird es geben. Das Wachstum der Spinnmilben ist über die Geburtenzahl positiv rückgekoppelt.
|
| |
|
|
|
|
|
|
|
|
Konstruiert ein Wachstumsmodell
für ein gleichförmiges Wachstum mit der Zustandsgröße "Spinnmilben", der Flussgröße Spinnmilben_Zunahme und dem Parameter Geburtenzahl.
Konstruiert ein Wachstumsmodell für ein unbegrenztes Wachstum mit der Zustandsgröße "Spinnmilben", der Flussgröße "Spinnmilben_Geburten" und dem Parameter "Geburtenrate_Spinnmilbe".
Beschreibt die Dynamiken der Wachstumsmodelle in Flussdiagrammen.
| |
Bei der folgenden dynamischen - also zeitabhängigen - Modellierung des Wachstums der „Spinnmilben“ quantifizieren wir die qualitativen Beschreibungen in Flussdiagrammen.
Fall A: Die Spinnmilbenpopulation (S) nimmt täglich konstant zu. Die Geburtenzahl z.B. von 50 Milben erzeugt eine tägliche Spinnmilben_Zunahme (SZ).
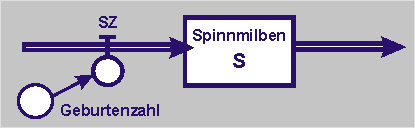
Fall B:
Das Wachstum der „Spinnmilben“ (S) ist über die Geburtenzahl positiv rückgekoppelt.
Die Spinnmilben-Geburten (SG) hängen von der Geburtenrate (g) sowie von der Anzahl der bereits lebenden Spinnmilben ab.
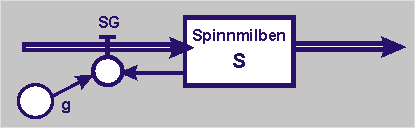
|
|
|
|
| Beschreibt die beiden Modelle durch eine Zustandsgleichung und ggf. durch eine weitere Modellgleichung.
Zustandsgröße: "Spinnmilben" S
Flussgrößen: Zunahme_Spinnmilben SZ
Spinnmilben_Geburten SG
Raten: Geburtenrate g | |
Fall A: Den Wachstumsprozess beschreiben wir unter Berücksichtigung eines Zeittaktes zwischen dem Zustand_neu und Zustand_alt in der folgenden Zustandsgleichung.
S_neu <-- S_alt + Δt · SZ;
In Worten: Der neue Zustand der Spinnmilben (S_neu) ergibt sich immer wieder aus dem alten Zustand der Spinnmilben( S_alt) plus Zeittakt mal Spinnmilben_Zunahme (SZ.)
Anfangsgröße für S = 100; Δt = 1 (Zeittakt = 1Tag);
SZ (Spinnmilben_Zunahme) = Geburtenzahl = 50 (pro Tag)
Fall B: Die vorhergehende Zustandsgleichung ändern wir in Bezug auf die Spinnmilben_Zunahme. Sie wird zur Anzahl der Spinnmilben_Geburten (SG) und diese berechnen wir aus der Anzahl der bereits lebenden Spinnmilben und der Geburtenrate g.
S_neu <-- S_alt + Δ t · SG;
Anfangsgröße für S = 100; Δt = 1 (Zeittakt = 1Tag);
SG = g · S; g = 0,29
|
|
|
|
| Programmiert die beiden Wachstumsmodelle in einer Excel-Tabelle. |
|
Fall A siehe:
ExcelDateien/Mappe1918a.htm (zur Ansicht) oder ExcelDateien/Mappe1918a.xls (herunterladbar und interaktiv)
Fall B siehe:
ExcelDateien/Mappe1918b.htm (zur Ansicht) oder ExcelDateien/Mappe1918b.xls (herunterladbar und interaktiv)
|
| |
|
|
| Überlegt euch, wie ihr die Geburtenrate der Spinnmilben bestimmen könnt. |
|
„Von einer Spinnmilbenpopulation sind 75% weiblich. Eine erwachsene Spinnmilbe legt wöchentlich ca. 50 Eier von denen sich unter Gewächshausbedingungen durchschnittlich 80% nach 2 Wochen zu erwachsenen Insekten entwickeln ....“
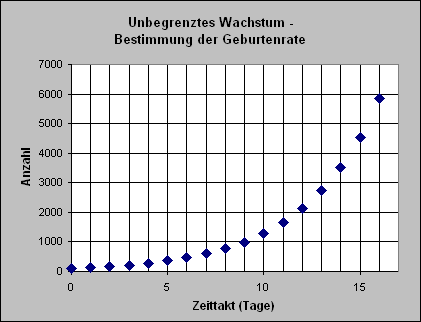
Auf der Grundlage dieser Sachinformation ist folgende rechnerische Abschätzung für die Geburtenrate möglich: Von 100 Spinnmilben sind 75 weiblich. Sie entwickeln in 14 Tagen 75 · 4/5 · 50 = 3000 neue Milben. Genau diese Situation ist im folgenden Diagramm durch Simulation dargestellt. Simulativ finden wird so die Geburtenrate von g = 0,29 auf der Grundlage realer Daten. Die Geburtenrate kann aber auch höher sein, falls die Temperatur im Gewächshaus entsprechend ist. |
|
|
|
| Simuliert euer Wachstumsmodell
>>> nebenstehend
ein Simulationsergebnis
zum Fall B | |
 |
| |
|
|
Interpretiert die Simulationsergebisse und auch die Grenzen dieser Modelle. Schreibt eure Erkenntnisse auf und erstellt eine Präsentation.
|
|
Die Simulationsergebnisse zeigen uns, dass beide Modelle nicht realistisch sind. Einerseits wird es umso mehr Nachwuchs geben, je mehr Spinnmilben bereits leben. Die Entwicklung kann also nicht linear verlaufen. Andererseits sterben auch ständig Spinnmilben. Also muss bei der Entwicklung auch eine Sterberate berücksichtigt werden. |
|
|
|
|
|
Ungebremstes Wachstumsmodell
der Spinnmilben
unter Annahme einer Geburten- und Sterberate |
| |
|
|
Beschreibt die Dynamik eines ungebremsten Wachstums der Spinnmilben unter Annahme einer Geburten- und Sterberate in einem Wirkungsdiagramm.
|
|
Im folgenden Wirkungsdiagramm nehmen wir ( zusätzlich) an, dass die Spinnmilben nicht ewig leben. Einerseits haben die nachwachsenden Generationen immer wieder eine positive Wirkung auf die Geburtenzahl (Spinnmilben_Geburten). Andererseits sterben aber auch Spinnmilben eines natürlichen Todes. Und diese Sterbezahl (Spinnmilben_Todesfälle) wirkt negativ (abnehmend) auf die Spinnmilben-Population. Denn je mehr Spinnmilben es gibt, desto mehr werden auch sterben. |
| |
|
|
| |
|
 |
|
|
|
| Beschreibt die Dynamik dieses unbegrenzten Wachstums in einem Flussdiagramm. |
|
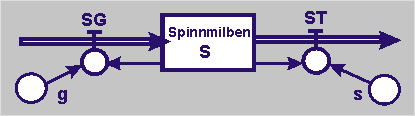
Bei der Übertragung des Wirkungsdiagramms in ein Flussdiagramm haben wir zur Quantifizierung sowohl eine Geburten- als auch eine Sterberate notwendig. |
| |
|
|
Zustandsgröße: "Spinnmilben" S
Flussgrößen:
"Spinnmilben_Geburt" SG und "Spinnmilben_Tod" ST
Parameter: "Geburtenrate_Spinnmilbe" g und "Sterberate_Spinnmilbe" s |
|
 |
|
|
|
| Beschreibt das Modell durch eine Zustands- und zwei weitere Modellgleichungen. |
|
Die folgende Zustandsgleichung und die folgenden zwei weiteren Modellgleichungen formulieren wir unter Berücksichtigung eines Zeittaktes zwischen Zustand_neu und Zustand_alt aus dem Flussdiagramm heraus.
S_neu <-- S_alt + Δ t · (SG - ST)
Anfangsgröße S = 100; Δt = 1 (Zeittakt = 1Tag)
Spinnmilben_Geburt = SG = g · S; Geburtenrate = g = 0,29
Spinnmilben_Tod = ST = s · S; Sterberate = s = 0,14
Wir nehmen die Sterberate halb so groß wie die Geburtenrate an, weil die Spinnmilben eine Lebensdauer von etwa 14 Tagen haben. Das ist das Zeitintervall indem aus 100 Milben 3000 neue entstehen. |
|
|
|
Programmiert das Wachstumsmodell in einer
Excel-Tabelle. |
|
Die Zustandsgleichung und die beiden Modellgleichungen programmieren wir in einer Excel-Tabelle. Zu diesem Zweck geben wir in den Spalten SG, ST und S_neu Formeln in Abhängigkeit von Δt, g und s sowie von der Anfangsgröße S ein. Zwar können wir die Zahlen in der Tabelle immer noch schrittweise selbstständig nachrechnen aber der Rechenaufwand ist jetzt schon extrem hoch, wenn bei jeder Änderung der Modellgrößen alle Werte neu errechnet werden müssen.
Siehe hierzu:
ExcelDateien/Mappe1918c.htm (zur Ansicht) oder ExcelDateien/Mappe1918c.xls (herunterladbar und interaktiv) |
|
|
|
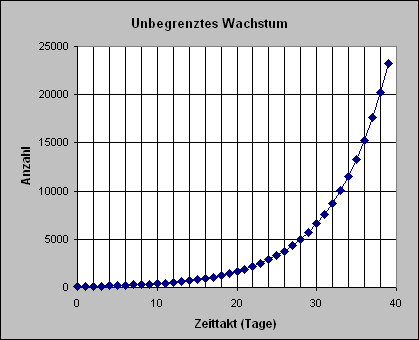
| Simuliert das Wachstumsmodell für unterschiedliche Raten.
>>> nebenstehend
ein Simulationsergebnis
| |
|
| |
|
|
| Überlegt euch, wie ihr die Geburtenrate und Sterberate der Spinnmilben bestimmen könnt. |
|
Die Geburtenrate einer konkreten Population von Spinnmilben in einer Plantage müsste „experimentell“ durch Abzählen an Pflanzen ermittelt werden. Denn „die Entwicklung verläuft über ein Ei- und 3 Jugendstadien bis zum adulten Tier und ist stark temperaturabhängig. Sie dauert bei 20°C ca. 17 Tage, bei 15 °C ca. 30 Tage. Das warme Gewächshausklima ist für die gemeine Spinnmilbe (Tetranychidae) ein idealer Lebensraum“.
Fassen wir die Geburtenrate und Sterberate zu einer Wachstumsrate (Wachstumsrate = Geburtenrate – Sterberate) zusammen, dann vereinfacht sich das letzte Modell auf eine Rückkopplung. |
|
|
|
| Beschreibt das Modell-Verhalten und interpretiert die Simulationsergebisse sowie die Grenzen dieses Modells.
Schreibt eure Erkenntnisse auf und erstellt eine Präsentation. | |
Die Spinnmilbenpopulation wächst in diesem Modell zunächst langsam, dann schneller. In immer kürzeren Zeitabständen verdoppelt sich die Anzahl der Spinnmilben. Und das kommt der Realität schon näher. Denn der stetig ansteigende Nachwuchs zeugt ebenfalls immer wieder Nachwuchs.
Jedoch, irgendwann werden die Spinnmilben alle Pflanzen kahl gefressen haben. Dann aber wird die Sterberate der Spinnmilben steigen und ihre Anzahl wird radikal abnehmen. Genau diese Überlegung zeigt uns die Grenzen des vorstehenden Modells auf.
Das Modell des „unbegrenzten Wachstums“ müsste also erneut überdacht und zu einem Modell des „begrenzten Wachstums“ erweitert werden. |
|
|
|
|
|
Gebremstes Wachstumsmodell von Spinnmilben
bei beschränkter Nahrung
|
| |
|
|
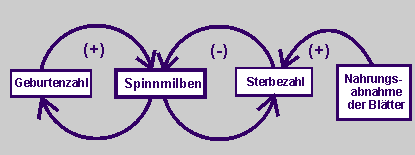
| Beschreibt die Dynamik eines begrenzten Wachstums der Spinnmilben bei beschränkter Nahrung zunächst in einem Wirkungsdiagramm. |
|
Wir nehmen jetzt an, dass der Vorrat an Blättern, also die Nahrungsmenge der Spinnmilben, schrittweise oder stetig abnimmt. Dann wirkt diese zunehmende Nahrungsknappheit positiv (verstärkend) auf die Sterbezahl. Sie wird „stetig“ größer. Das folgende Wirkungsdiagramm beschreibt in qualitativer Form ein begrenztes Wachstum der Spinnmilben. |
| |
|
|
| |
|
 |
|
|
|
| Übertragt das Wirkungsdiagramm in ein Flussdiagramm. |
|
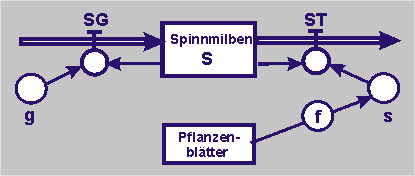
Die Dynamik können wir u.a. durch das folgende Flussdiagramm darstellen.
Die Verknappung der Nahrung können wir in unterschiedlicher Weise mit einer Funktion modellieren:
- a) mittels einer Treppenfunktion (Fall A) oder
- b) mittels einer linearen Funktion (Fall B)oder
- c) mittels einer quadratischen Funktion. ...
|
| |
|
|
| |
|
 |
|
|
|
| Beschreibt das Modell durch eine Zustands- und zwei weitere Modellgleichungen.
Zustandsgröße: "Spinnmilben" S
Flussgrößen:
"Spinnmilben_Geburt" SG und "Spinnmilben_Tod" ST
Parameter: "Geburtenrate_Spinnmilbe" g und "Sterberate_Spinnmilbe" s
Funktion: f | |
Die zunehmende Knappheit der Nahrung wird durch eine zeitabhängige Funktion f(t) quantifiziert.
S_neu <-- S_alt + Δ t · (SG - ST)
Anfangsgröße S = 100; Δt = 1 (Zeittakt = 1Tag)
SG = g · S; g = 0,35
ST = s · S · f(t); s = 0,17
Anmerkung: Die Geburtenrate und Sterberate habern wir gegenüber dem obigen Modell gleichmäßig vergrößert, aber immer noch im Rahmen rechnerischer Abschätzungen gehalten, wenn wir von höheren Temperaturen im Gewächshaus ausgehen.
Fall A: f(t) = 1 für die ersten drei Zeittakte,
f(t) = 1,5 für die nächsten drei Zeittakte
f(t) = 2 für die nächsten drei Zeittakte usw. ...
Fall B: f (t) = m · t, mit m= 0,1.
Anmerkung: Die Pflanzen könnten auch als eine weitere Zustandsgröße definiert werden, die in Abhängigkeit vom Wachstum der Spinnmilben steht. Dann hätten wir ein ähnliches Modell, wie es auf der nächsten Seite beschrieben wird. |
|
|
|
| Programmiert das Wachstums- modell in einer Excel-Tabelle. |
|
Fall A siehe:
ExcelDateien/Mappe1918d.htm (zur Ansicht) oder ExcelDateien/Mappe1918d.xls (herunterladbar und interaktiv)
Fall B siehe:
ExcelDateien/Mappe1918e.htm (zur Ansicht) oder ExcelDateien/Mappe1918e.xls (herunterladbar und interaktiv)
|
|
|
|
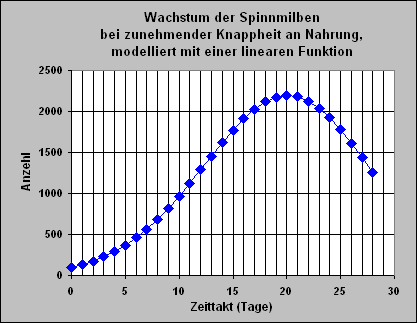
| Simuliert euer Wachstumsmodell für eine zunehmende Nahrungs- knappheit.
>>> nebenstehend
ein Simulationsergebnis
für den Fall B
| |
 |
|
|

|
| Beschreibt das Systemverhalten, interpretiert es und besprecht die Grenzen dieses Modells.
Schreibt eure Erkenntnisse auf und erstellt eine Präsentation. | |
Die Spinnmilbenpopulation wächst zunächst ständig schneller, solange genügend Nahrung vorhanden ist. Wird aber die Nahrungsmenge stetig knapper oder steigt die Nahrungsknappheit, so wächst die Population immer weniger. Sie erreicht schließlich ein Maximum und sinkt dann ggf. sehr schnell bis zum Aussterben ab.
Es ist zu fragen: Was soll mit dem Modell und seinen Simulationen bewirkt werden?
Geht es darum, im Gewächshaus sinnvoll handeln zu können oder geht es schlichtweg nur darum, eine allgemeine, qualitative Erkenntnis über die Dynamik von Wachstumsprozessen (u.a. bei Spinnmilben) zu erlangen? Von der Antwort hängt ab, welche Sorgfalt ggf. darauf gelegt werden muss, Anfangsgrößen und Wachstumsgrößen experimentell im Gewächshaus zu bestimmen. Dieser Gedanke wird auch auf der nächsten Seite noch fortgesetzt und vertieft.
Siehe aber auch die mathematische Hilfeseite "Wachstum einer Population auf begrenzter Fläche". |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |






















